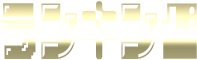X=2a+b
Y=2a+3b
という2つの式で表すことができ、
「a,b,X,Yはそれぞれ特定の素数である時に成立する」
という法則があることを知っていた。
しかし最近になって、
「Xが素数でなくても、いくつであっても成立する場合がある」
という理論があることを知った。
この理論を特に何と言う?
※意味が大体合っていれば正解とします。


出題完了、よかったら評価していってください。

(a,b,X,Y)=(2,3,7,13)のときに与式を満たすことは重要ですか?

NO その組み合わせではありません(数字は部分的に合っています) [編集済]
「いくつであっても」は年齢のことを指していますか? [編集済]

NO 年齢ではありません。ちなみにプリモは中学三年生らしいです、つまりこの問題は中学三年生なら解けると思います。
Xは俳句(五七五)の文字数、Yは短歌(五七五七七)の文字数を表しており、「Xがいくつであっても成立する場合」は文字数に決まりのない自由律俳句を指していますか? [編集済]


YES! 正解です! [正解][良い質問]
3/25 19時 まとメモを更新しました。
3/26 14時 まとメモを更新しました。[編集済]

X,Y,a,bに入る素数はすべてアラビア数字と考えて成立しますか?

YES? 単なる数値としてならアラビア数字でも成立しますが、漢数字の方がわかりやすいです。 [良い質問]
XとYは言葉に置き換えることができますか?

YES! XとYは言葉を数字に置き換えたものであり、さらに別の日本語に置き換えることができます。(説明がわかりにくくてすみません、ミスリード注意です) [良い質問]
Xは川柳、俳句でYは短歌を表していますか?

YES! 中学生のプリモ君が最近知ったという「いくつでも成立する俳句」をお答えください。 [良い質問]

プリモ君は国語の授業で俳句や短歌について学んだが、俳句は別に17文字きっかりじゃなくてもいいと知りましたか?(a=5,b=7,X=17,Y=31)

YES! 正解です! プリモ君が知ったのは「自由律俳句」でした。 [正解][良い質問]
具体的な一つの自由律俳句を答える必要がありますか?


NO! 「自由律俳句」「自由律」「破調」「字余り」「字足らず」などが正解になります、つまりこの質問も正解です! (「XとYは何か?」だと別解が多すぎるのでこのような形にしました) [正解][良い質問]

理論を何と言う?なので自由律俳句と答えるべきでしたね


「字余り」「字足らず」などの概念でも正解です、「XとYは何か?」だと別解が多すぎると思ってこの形式にしましたが、これ以降は「俳句」「川柳」「和歌」などのワードが出た時点で正解にするようにします。 [良い質問]

理論を何と言う?なので自由律俳句と答えるべきでしたね…。17と31が全くの別分野でこんな繋がりがあるとは…。とても面白かったです!出題ありがとうございました!


こちらこそ! ご参加頂きありがとうございます! [良い質問]
数学の知識は必要ですか?

NO! 数学ではない学問の知識が必要です、素数については「素数 一覧」で検索するだけで充分です。 [良い質問]

問われている理論においてXの値を変動させたとしても、Yの値は31で固定ですか? [編集済]

YES NO 答えにくいのですが、XとYは「関係あるようなないような」といった感じの関係なので、XとYの値は連動しません、しかし、「Xがいくつでも成立する」という理論をYに対しても適用すれば「Yはいくつでも成立する」ということになります。「Yはいくつでも成立する」という理論の方は知名度が低いです。 [良い質問]

Xの式は俳句、Yの式は短歌の文字数について述べていますか? [編集済]

YES! 重要なキーワードが出たので正解です! 「この理論」は「自由律」のことです。 [正解][良い質問]
Yは五七五七七で三十一文字の短歌
「文字数が自由な俳句」は「自由律」または「自由律俳句」または「破調」
頭が理系な留学生のプリモ君はそれまで定形の俳句しか知らなかったが、最近になって国語の授業で自由律俳句を知った。
※「XとYは何か?」という形式にしなかったのは、私の知らない七五調の何かを答えられた時にそれが正解か不正解かを判断できる自信がなかったからです。
参加者一覧 6人








「プリモ君」という謎のキャラクターが急に現れて困惑している人もいるかもしれないので説明します、「プリモ君」は既存のキャラクターではありません、イタリア語で「素数」を意味する「numero primo」から名付けた、この問題専用の人物です。[22年03月20日 00:00]



追記 素数については「素数 一覧」で検索して確認してください、あとは問題文の2つの計算式を理解できていれば、数学についての他の知識は全く不要です。
追記 この理論は中学三年生で学習するらしいです。
自分が正解した問題・出題者への賛辞・シリーズ一覧・良い進行力など、基準は人それぞれです。
自分専用のブックマークとしてお使い下さい。
Goodって?
「トリック」「物語」「納得感」そして「良質」の4要素において「好き」を伝えることができます。
これらの要素において、各々が「良い」と判断した場合にGoodしていきましょう。
ただし進行力は評価に含まれないものとします。
ブクマ・Goodは出題者にとってのモチベーションアップに繋がります!「良い」と思った自分の気持ちは積極的に伝えていこう!